Unified Mathematics for Hybrid Systems

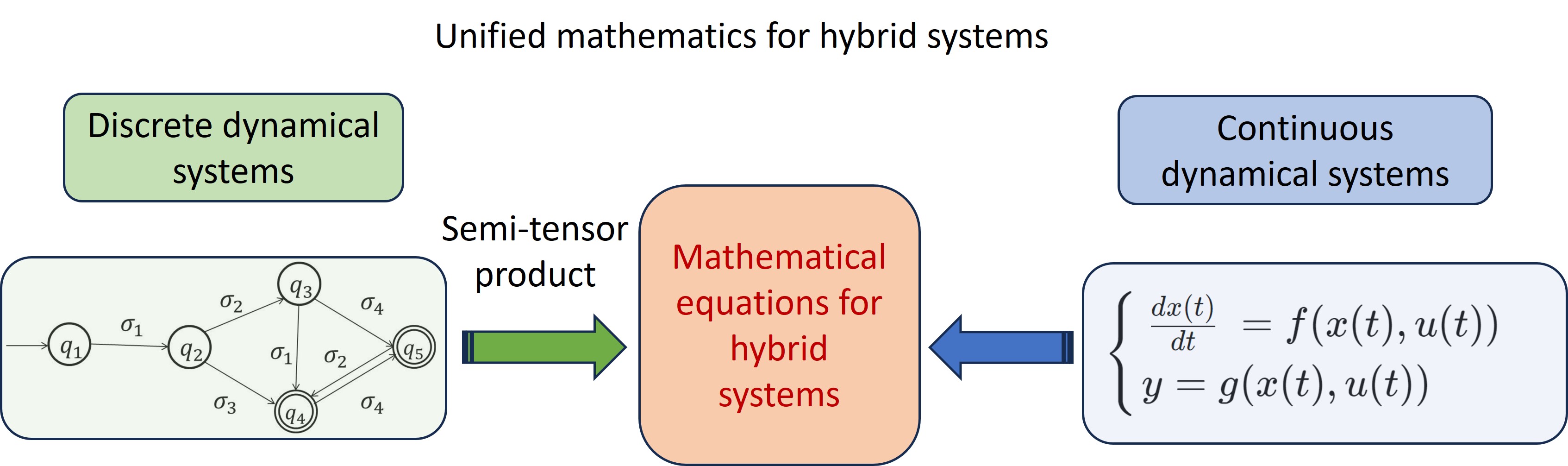
As we know, continuous dynamics and logic do not exist alone in the real world. An interesting topic is how to model hybrid systems with logic by mathematical expressions. In light of semi-tensor product (STP) and differential equations, we first constructed the model of complex networks with continuous dynamics and Boolean logic and further analyzed its synchronization. Member of European Academy of Sciences, IEEE fellow Prof. Jinde Cao commented on our work in his published paper: “Recently, the network-based dynamical system has been found to be an interesting research topic together with novel techniques (see [47] and [48]). …, the accomplished results and offered techniques in [47] and [48] have been discovered very broad and exceptionally helpful to promote further investigations on these issues.” The mentioned literature [48] is this work. Next, we also formulated a framework to describe hybrid systems driven by automata (HSDA) based on the STP technique and equations, where the evolutions of automata, continuous dynamics, and their interactions were well depicted in a unified way.